Welcome to this week’s Math Munch!
 I just ran across a website that’s chock full of cool math applets, links, and craft ideas – and perfect for fulfilling those summer math cravings! Math Cats was created by teacher and parent Wendy Petti to, as she says on her site, “promote open-ended and playful explorations of important math concepts.”
I just ran across a website that’s chock full of cool math applets, links, and craft ideas – and perfect for fulfilling those summer math cravings! Math Cats was created by teacher and parent Wendy Petti to, as she says on her site, “promote open-ended and playful explorations of important math concepts.”
Math Cats has a number of pages of interesting mathematical things to do, but my favorite is the Math Cats Explore the World page. Here you’ll find links to cool math games and explorations made by Wendy, such as…
 … the Crossing the River puzzle! In this puzzle, you have to get a goat, a cabbage, and a wolf across a river without any of your passengers eating each other! And…
… the Crossing the River puzzle! In this puzzle, you have to get a goat, a cabbage, and a wolf across a river without any of your passengers eating each other! And…
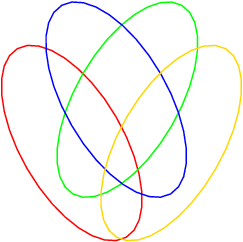
 … the Encyclogram! Make beautiful images called harmonograms, spirographs, and lissajous figures with this cool applet. Wendy explains some of the mathematics behind these images, too. And, one of my favorites…
… the Encyclogram! Make beautiful images called harmonograms, spirographs, and lissajous figures with this cool applet. Wendy explains some of the mathematics behind these images, too. And, one of my favorites…
 … Scaredy Cats! If you’ve ever played the game NIM, this game will be very familiar. Here you play against the computer to chase cats away – but don’t be left with the last cat, or you’ll lose!
… Scaredy Cats! If you’ve ever played the game NIM, this game will be very familiar. Here you play against the computer to chase cats away – but don’t be left with the last cat, or you’ll lose!
These are only a few of the fun activities to try on Math Cats. If you happen to be a teacher or parent, I recommend that you look at Wendy’s Idea Bank. Here Wendy has put together a very comprehensive and impressive list of mathematics lessons, activities, and links contributed by many teachers.

Next, Vi Hart has a new video that showcases one of my favorite things in mathematics – the frieze. A frieze is a pattern that repeats infinitely in one direction, like the footsteps of the person walking in a straight line above. All frieze patterns have translation symmetry – or symmetry that slides or hops – but some friezes have additional symmetries. The footsteps above also have glide reflection symmetry – a symmetry that flips along a horizontal line and then slides. Frieze patterns frequently appear in architecture. You can read more about frieze patterns here.
Reading about frieze patterns is all well and good – but what if you could listen to them? What would a translation sound like? A glide reflection? The inverse of a frieze pattern? Vi sings the sounds of frieze patterns in this video.
[youtube http://www.youtube.com/watch?v=Av_Us6xHkUc&feature=BFa&list=UUOGeU-1Fig3rrDjhm9Zs_wg]
Do you have your own take on frieze music? Send us your musical compositions at MathMunchTeam@gmail.com .
Finally, if I were to ask you to name the number directly in the middle of 1 and 9, I bet you’d say 5. But not everyone would. What would these strange people say – and why would they also be correct? Learn about this and some of the history, philosophy, and psychology of numbers – and hear some great stories – in this podcast from Radiolab. It’s called Numbers.

Bon appetit!
P.S. – Paul made a new Yoshimoto video! The Mega-Monster Mesh comes alive! Ack!
[youtube https://www.youtube.com/watch?v=PMpr8pA5lJw&feature=player_embedded]
P.P.S. – Last week – June 28th, to be exact – was Tau Day. For more information about Tau Day and tau, check out the last bit of this old Math Munch post. In honor of the occasion, Vi Hart made this new tau video. And there’s a remix.
 The second contest is for high schoolers and is called Math-O-Vision. The challenge is to make a video that shows “the way Math fills our world.” Math-O-Vision is sponsored by the Dartmouth College Math Department and the Neukom Institute.
The second contest is for high schoolers and is called Math-O-Vision. The challenge is to make a video that shows “the way Math fills our world.” Math-O-Vision is sponsored by the Dartmouth College Math Department and the Neukom Institute. Finally, here’s a fun little applet I found called Make-a-Flake. You can use it to make intricate digital snowflake designs.
Finally, here’s a fun little applet I found called Make-a-Flake. You can use it to make intricate digital snowflake designs.