Welcome to this week’s Math Munch – from the Netherlands!
I’m at the Bridges Mathematical Art Conference, which this year is being held in Enschede, a city in the Netherlands. I’ve seen so much beautiful mathematical artwork, met so many wonderful people, and learned so many interesting new things that I can’t wait to start sharing them with you! In the next few weeks, expect many more interviews and links to sites by some of the world’s best mathematical artists.
But first, have a look at some of the artwork from this year’s art gallery at Bridges.
Here are three pieces that I really love. The first is a crocheted hyperbolic plane lampshade. I love to crochet hyperbolic planes (and we’ve posted about them before), and I think the stitching and lighting on this one is particularly good. The second is a bunny made out of the word bunny! (Look at it very closely and you’ll see!) It was made by one of my favorite mathematical artists, Henry Segerman. Check back soon for an interview with him!
This last is a curious sculpture. From afar, it looks like white arcs surrounding a metal ball, but up close you see the reflection of the arcs in the ball – which make a hexagonal flower! I love how this piece took me by surprise and played with the different ways objects look in different dimensions.
 Mathematical artists also talk about their work at Bridges, and one of the talks I attended was by Jack van Wijk, a professor from Eindhoven University of Technology in the Netherlands. Jack works with data visualization and often uses a mixture of math and images to solve complicated problems.
Mathematical artists also talk about their work at Bridges, and one of the talks I attended was by Jack van Wijk, a professor from Eindhoven University of Technology in the Netherlands. Jack works with data visualization and often uses a mixture of math and images to solve complicated problems.
One of the problems Jack tackled was the age-old problem of drawing an accurate flat map of the Earth. The Earth, as we all now know, is a sphere – so how do you make a map of it that fits on a rectangular piece of paper that shows accurate sizes and distances and is simple to read?
 To do this, Jack makes what he calls a myriahedral projection. First, he draws many, many polygons onto the surface of the Earth – making what he calls a myriahedron, or a polyhedron with a myriad of faces.
To do this, Jack makes what he calls a myriahedral projection. First, he draws many, many polygons onto the surface of the Earth – making what he calls a myriahedron, or a polyhedron with a myriad of faces. 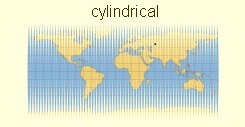 Then, he decides how to cut the myriahedron up. This can be done in many different ways depending on how he wants the map to look. If he wants the map to be a nice, normal rectangle, maybe he’ll cut many narrow, pointed slits at the North and South Poles to make a map much like one we’re used to. But, maybe he wants a map that groups all the continents together or does the opposite and emphasizes how the oceans are connected…
Then, he decides how to cut the myriahedron up. This can be done in many different ways depending on how he wants the map to look. If he wants the map to be a nice, normal rectangle, maybe he’ll cut many narrow, pointed slits at the North and South Poles to make a map much like one we’re used to. But, maybe he wants a map that groups all the continents together or does the opposite and emphasizes how the oceans are connected…
Jack made a short movie that he submitted to the Bridges gallery. He animates the transformation of the Earth to the map projections beautifully.
Jack’s short movie wasn’t the only great film I saw at Bridges. The usual suspects – Vi Hart and her father, George Hart – also submitted movies. George’s movie is about a math topic that I find particularly fascinating: juggling! The movie stars professional juggler Rod Kimball. Click on the picture below to watch:
This is only the tip of the iceberg that is the gorgeous and interesting artwork I saw at Bridges. Check out the gallery to see more (including artwork by our own Paul and a video by Paul and Justin!), or visit Math Munch again in the coming weeks to learn more about some of the artists.
Bon appetit!




The juggling video was very interesting, i didn’t know juggling required so much math! I learned that the 5 1 pattern creates a type of spiral braid when you tie a ball to a piece of string, and juggle it.
I didn’t know you could make so many shapes with a sphere! It looks really cool with a pattern that is familiar to everyone.
When I began watching this confusing video I learned that juggling has to do with math because it requires a a lot of patterns .Once you throw a ball into your juggling you need to throw it 9 times higher then it was before in the end I really took interested in this video.
I didn’t know juggling required math! But as I watched the juggling video, juggling has a bunch of patterns. You have throw the first ball high up, and then throw the second ball low in order to catch them both at the same time. I also didn’t know that when you juggle three balls, it makes a type of braid. This was a very interesting video.
Wow that is just amazing! i loved that last unfold, it looked a lot like a sunflower! Most of these patterns will be too difficult to even cut because if you cut it too thin it will rip. I really want to try this!! who came up with this? And how did they do all the tricky cuts? And also, how many patterns are there really?
How can you just unfold the earth like that? I don’t understand on how at the end of the video the folds become bigger.
Hi Julie! I see what you mean about the folds becoming bigger towards the end of the video. The pieces at the beginning are very long and skinny, whereas the pieces at the end are sort of fatter. If you look really carefully, though, you can see slits and cracks in the bigger pieces that actually break them up. To lie a big chunk of sphere flat you need to make lots of tiny cracks in it (ever tried to flatten a big pieces of orange peel?) – you can kind of see then if you look really closely at the video. Does that help?
I thought it was cool that nobody else thought of just simply unfolding the globe to make a better map, and a more accurate map and I like that it’s a whole new idea. How their were different ways to show it and unfold it like cutting it so all the continents were together or to show that all the oceans were connected, was also really cool. I like how the idea is so out side the box but also so inside as well. It’s so inside because it’s so simple to just unfold it. But then it’s so out side the box because no one else thought to do that and I haven’t seen anything like it.
Hi Teresa! It is cool, isn’t it? Your observation that just unfolding the Earth is such a simple idea, but so outside the box from how we normally think about making maps, is really interesting. I feel like unfolding the Earth might sound like a radical way to make maps because people thought that the Earth was flat for a long time. If the Earth is flat, there’s no need to unfold the surface of a sphere. But it isn’t flat, so drawing it as flat is very inaccurate. Thanks for your thoughtful comment!
i didn’t realize that juggling required so much math or that it was related to braiding. The part where it showed the different braids made by the balls attached to string helped me understand the pattern better.
Hi Ashley! I really like the visualization, too. It’s hard to see the braid unless you really see the braid. Thanks for your comment!
I found it interesting that you could unfold the earth in all of those ways. I had never thought of making a 2-dimensional map of the earth in any other way than the standard map.
in the video of the man juggling I liked how he showed how high the a ball can go and when it dropped. then in the videos they showed if you juggle 3 balls at a time it should be in a certain pattern. the patterns were my favorite part.
I thought that the last shape that you could make with the coastlines of the world was pretty cool, because it reminded me of a drawing of the sun from a different era.
This was a interesting video how all the possible combinations in juggling are. But I found the math behind the juggling to be in different and unique patterns
this video was interesting and cool because the guy knew how to juggle, though it will be nice if I knew how to juggle too. And I kind of know how this is related to math munch.
Pingback: Near Miss, Curiosa Mathematica, and Poincaré | Math Munch