Welcome to this week’s Math Munch!
The Summer Olympics are underway in Brazil. I have loved the Olympics since I was a kid. The opening ceremony is one of my favorite parts—the celebration of the host country’s history and culture, the athletes proudly marching in and representing their homeland. And the big moment when the Olympic cauldron is lit! This year I was just so delighted by the sculpture that acted as the cauldron’s backdrop.
Isn’t that amazing! The title of this enormous metal sculpture is Lucea, and it was created by American sculptor Anthony Howe. You can read about Anthony and how he came to make Lucea for the Olympics in this article. Here’s one quote from Anthony:
“I hope what people take away from the cauldron, the Opening Ceremonies, and the Rio Games themselves is that there are no limits to what a human being can accomplish.”
Here’s another view of Lucea from Anthony’s website:
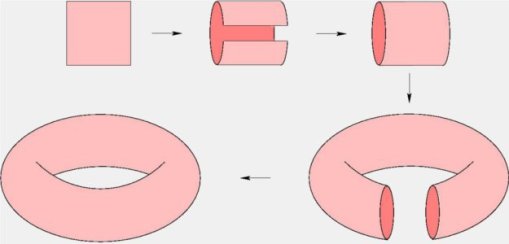
Lucea is certainly hypnotizing in its own right, but I think it jumped out at me in part because I’ve been thinking a lot about fiber bundles recently. A fiber bundle is a “twist” on a simpler kind of object called a product space. You are familiar with some examples of products spaces. A square is a line “times” a line. A cylinder is a line “times” a circle. And a torus is a circle “times” a circle.
So, what does it mean to introduce a “twist” to a product space? Well, it means that while every little patch of your object will look like a product, the whole thing gets glued up in some fancy way. So, instead of a cylinder that goes around all normal, we can let the line factor do a flip as it goes around the circle and voila—a Mobius strip!
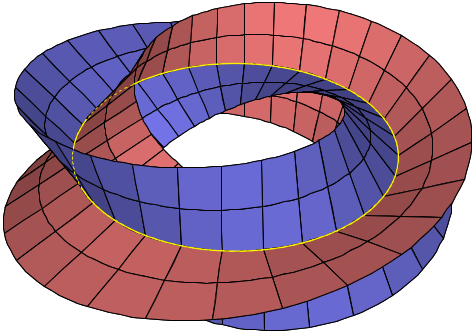
Now, check out this image:
It’s two Mobius strips stuck together! Does this remind you of Lucea?! Instead of a line “times” a circle that’s been twisted, we have an X shape “times” a circle.
Do you think you could fill up all of space with an infinity of circles? You might try your hand at it. One answer to this puzzle is a wonderful example of a fiber bundle called the Hopf fibration. Just as you can think about a circle as a line plus one extra point to close it up, and a sphere as a plane with one extra point to close it up, the three-sphere is usual three-dimenional space plus one extra point. The Hopf fibration shows that the three-sphere is a twisted product of a sphere “times” a circle. For a really lovely visualization of this fact, check out this video:
That is some tough but also gorgeous mathematics. Since you’ve made it this far in the post, I definitely think you deserve to indulge and maybe rock out a little. And what’s the hottest ticket on Broadway this summer? I hope you’ll enjoy this superb music video about Hamilton!
William Rowan Hamilton, that is. The inventor of quaternions, explorer of Hamiltonian circuits, and reformulator of physics. Brilliant.
 Here are a couple of pages of Hamiltonian circuit puzzles. The goal is to visit every dot exactly once as you draw one continuous path. Try them out! Rio, where the Olympics is happening, pops up as a dot in the first one. You might even try your hand at making some Hamiltonian puzzles of your own.
Here are a couple of pages of Hamiltonian circuit puzzles. The goal is to visit every dot exactly once as you draw one continuous path. Try them out! Rio, where the Olympics is happening, pops up as a dot in the first one. You might even try your hand at making some Hamiltonian puzzles of your own.
Happy puzzling, and bon appetit!