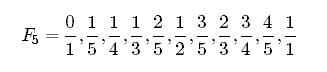Welcome to this week’s Math Munch!
Check out this awesome graph:
What is it? It’s a graph of the Farey Fractions, with the denominator of the (simplified) fraction on the vertical axis and the value of the fraction on the horizontal axis, made by mathematician and professor at Wheelock College Debra K. Borkovitz (previously). Now, I’d never heard of Farey Fractions before I saw this image – but the graph was so cool that I wanted to learn all about them!
So, what are Farey Fractions, you ask? Debra writes all about them and the cool visual patterns they make in this post. To make a list of Farey Fractions you first pick a number – say, 5. Then, you list all of the fractions between 0 and 1 whose denominators are less than or equal to the number you picked. So, as Debra writes in her post, for 5 the list of Farey Fractions is:
As Debra writes, there are so many interesting patterns in Farey Fractions – many of which become much easier to see (literally) when you make a visualization of them. Debra has made several awesome applets using the program GeoGebra, which she links to in her post. (You can download GeoGebra and make applets of your own by visiting our Free Math Software page.) These applets really show the power of using graphs and pictures to learn more about numbers. To play with the applet that made the picture above, click here. Check out her post to play with another applet, and to read more about the interesting patterns in Farey Fractions.
 Next, check out this website devoted to the puzzles of puzzlemaster Sam Loyd. Sam Loyd was a competitive chess player and professional puzzle-writer who lived at the end of the nineteenth century. He wrote many puzzles that are still famous today – like the baffling Get Off the Earth puzzle. Click the link to play an interactive version of the Get Off the Earth puzzle.
Next, check out this website devoted to the puzzles of puzzlemaster Sam Loyd. Sam Loyd was a competitive chess player and professional puzzle-writer who lived at the end of the nineteenth century. He wrote many puzzles that are still famous today – like the baffling Get Off the Earth puzzle. Click the link to play an interactive version of the Get Off the Earth puzzle.
The site has links to numerous Sam Loyd puzzles. Check out the Picture Puzzles, in which you have to figure out what object is described by the picture, or the Puzzleland Puzzles, which feature characters from the fictional place Puzzleland that Sam created.

Snow MArTH, made by MArTHist Eva Hild and others at a snow sculpture event in Colorado. From the Spring, 2011 Hyperseeing.
Finally, take a look at some of the beautiful pictures and fascinating articles in this journal about mathematical art (a.k.a., MArTH) called Hyperseeing. Hyperseeing is edited by mathematicians and artists Nat Friedman and Ergun Akleman. Hyperseeing is published by the International Society of the Arts, Mathematics, and Architecture, which Nat founded to encourage education connecting the arts, architecture, and math – which we here at Math Munch love! In one of his articles, Nat defines hyperseeing as, “Interdisciplinary education… concerned with seeing from multiple viewpoints in a very general sense. Hyperseeing is a more complete way of seeing.”
There are so many beautiful images to look at and interesting articles to read in Hyperseeing. Among other things, each edition of Hyperseeing features a mathematical comic by Ergun. Here are some of my favorite Hyperseeings from the archives:
 This edition of Hyperseeing features crocheted hyperbolic surfaces (which we featured not long ago in this Math Munch!) and sculptures made with a 3-D printer, among many other things. |
Bon appetit!
P.S. – You may have noticed a new thing to click off to the right, below the Favorite Munches. This is our For Teachers section. The Math Munch team has put together several pages to describe how we use Math Munch in our classes and give suggestions for how you might use it, too. Teachers and non-teachers alike may want to check out our new Why Math Munch? page, which gives our mission statement.
P.P.S. – The Math Munch team is going to Bridges on Thursday! Maybe we’ll see you there.