Tag Archives: primes

Prime Gaps, Mad Maths, and Castles

Welcome to this week’s Math Munch!

It has been a thrilling last month in the world of mathematics. Several new proofs about number patterns have been announced. Just to get a flavor for what it’s all about, here are some examples.

I can make 15 by adding together three prime numbers: 3+5+7. I can do this with 49, too: 7+11+31. Can all odd numbers be written as three prime numbers added together? The Weak Goldbach Conjecture says that they can, as long as they’re bigger than five. (video)

11 and 13 are primes that are only two apart. So are 107 and 109. Can we find infinitely many such prime pairs? That’s called the Twin Prime Conjecture. And if we can’t, are there infinitely many prime pairs that are at most, say, 100 apart? (video, with a song!)

Harald Helfgott

Yitang “Tom” Zhang

People have been wondering about these questions for hundreds of years. Last month, Harald Helfgott showed that the Weak Goldbach Conjecture is true! And Yitang “Tom” Zhang showed that there are infinitely many prime pairs that are at most 70,000,000 apart! You can find lots of details about these discoveries and links to even more in this roundup by Evelyn Lamb.

What’s been particularly fabulous about Tom’s result about gaps between primes is that other mathematicians have started to work together to make it even better. Tom originally showed that there are an infinite number of prime pairs that are at most 70,000,000 apart. Not nearly as cute as being just two apart—but as has been remarked, 70,000,000 is a lot closer to two than it is to infinity! That gap of 70,000,000 has slowly been getting smaller as mathematicians have made improvements to Tom’s argument. You can see the results of their efforts on the polymath project. As of this writing, they’ve got the gap size narrowed down to 12,006—you can track the decreasing values down the page in the H column. So there are infinitely many pairs of primes that are at most 12,006 apart! What amazing progress!

Two names that you’ll see in the list of contributors to the effort are Andrew Sutherland and Scott Morrison. Andrew is a computational number theorist at MIT and Scott has done research in knot theory and is at the Australian National University. They’ve improved arguments and sharpened figures to lower the prime gap value H. They’ve contributed by doing things like using a hybrid Schinzel/greedy (or “greedy-greedy”) sieve. Well, I know what a sieve is and what a greedy algorithm is, but believe me, this is very complicated stuff that’s way over my head. Even so, I love getting to watch the way that these mathematicians bounce ideas off each other, like on this thread.

Andrew Sutherland

Click through to see Andrew next to an amazing Zome creation!

Andrew. Click this!

Scott Morrison

Andrew and Scott have agreed to answer some of your questions about their involvement in this research about prime gaps and their lives as mathematicians. I know I have some questions I’m curious about! You can submit your questions in the form below:

I can think of only two times in my life where I was so captivated by mathematics in the making as I am by this prime gaps adventure. Andrew Wiles’s proof of Fermat’s Last Theorem was on the fringe of my awareness when it came out in 1993—its twentieth anniversary of his proof just happened, in fact. The result still felt very new and exciting when I read Fermat’s Enigma a couple of years later. Grigori Perelman’s proof of the Poincare Conjecture made headlines just after I moved to New York City seven years ago. I still remember reading a big article about it in the New York Times, complete with a picture of a rabbit with a grid on it.

This work on prime gaps is even more exciting to me than those, I think. Maybe it’s partly because I have more mathematical experience now, but I think it’s mostly because lots of people are helping the story to unfold and we can watch it happen!

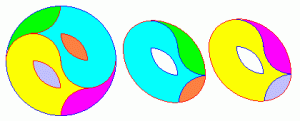Next up, I ran across a great site the other week when I was researching the idea of a “cut and slide” process. The site is called Mad Maths and the page I landed on was all about beautiful dissections of simple shapes, like circles and squares. I’ve picked out one that I find especially charming to feature here, but you might enjoy seeing them all. The site also contains all kinds of neat puzzles and problems to try out. I’m always a fan of congruent pieces problems, and these paper-folding puzzles are really tricky and original. (Or maybe, origaminal!) You’ll might especially like them if you liked Folds.

Christian’s applet displaying the original four-room castle.

Finally, we previously posted about Matt Parker’s great video problem about a princess hiding in a castle. Well, Christian Perfect of The Aperiodical has created an applet that will allow you to explore this problem—plus, it’ll let you build and try out other castles for the princess to hide in. Super cool! Will I ever be able to find the princess in this crazy star castle I designed?!

My crazy star castle!

And as summer gets into full swing, the other kind of castle that’s on my mind is the sandcastle. Take a peek at these photos of geometric sandcastles by Calvin Seibert. What shapes can you find? Maybe Calvin’s creations will inspire your next beach creation!

Bon appetit!

Posted by Justin Lanier. Categories: Math Munch. Tags: applet, arithmetic, big numbers, building, geometry, interactive puzzle, interview, numbers, origami, primes, puzzles, recreational mathematics, sandcastles, video. 6 Comments

Apr. ’13

“Happy Birthday, Euler!”, Project Euler, and Pants

Welcome to this week’s Math Munch!

Did you see the Google doodle on Monday?

This medley of Platonic solids, graphs, and imaginary numbers honors the birthday of mathematician and physicist Leonhard Euler. (His last name is pronounced “Oiler.” Confusing because the mathematician Euclid‘s name is not pronounced “Oiclid.”) Many mathematicians would say that Euler was the greatest mathematician of all time – if you look at almost any branch of mathematics, you’ll find a significant contribution made by Euler.

Euler was born on April 15, 1707, and he spent much of his life working as a mathematician for one of the most powerful monarchs ever, Frederick the Great of Prussia. In Euler’s time, the kings and queens of Europe had resident mathematicians, philosophers, and scientists to make their countries more prestigious. The monarchs could be moody, so mathematicians like Euler had to be careful to keep their benefactors happy. (Which, sadly, Euler did not. After almost 20 years, Frederick the Great’s interests changed and he sent Euler away.) But, the academies helped mathematicians to work together and make wonderful discoveries.

Want to read some of Euler’s original papers? Check out the Euler Archive. Here’s a little bit of an essay called, “Discovery of a Most Extraordinary Law of Numbers, Relating to the Sum of Their Divisors,” which you can find under the subject “Number Theory”:

Mathematicians have searched so far in vain to discover some order in the progression of prime numbers, and we have reason to believe that it is a mystery which the human mind will never be able to penetrate… This situation is all the more surprising since arithmetic gives us unfailing rules, by means of which we can continue the progression of these numbers as far as we wish, without however leaving us the slightest trace of any order.

Mathematicians still find this baffling today! If you’re interested in dipping your toes into Euler’s writings, I’d suggest checking out other articles in “Number Theory,” such as “On Amicable Numbers,” or some articles in “Combinatorics and Probability,” like “Investigations on a New Type of Magic Square.”

Want to work, like Euler did, on important math problems that will stretch you to make connections and discoveries? Check out Project Euler, an online set of math and computer programming problems. You can join the site and, as you work on the problems, talk to other problem-solvers, contribute your solutions, and track your progress. The problems aren’t easy – the first one on the list is, “Find the sum of all the multiples of 3 and 5 below 1000” – but they build on one another (and are pretty fun).

pants200-8bb43915cd34ea1718d8fe4716cf33c5e60a5a2d-s3

Pants made from a crocheted model of the hyperbolic plane, by Daina Taimina.

Finally, if someone asked you what a pair of pants is, you probably wouldn’t say, “a sphere with three open disks removed.” But maybe you also didn’t know that pants are important mathematical objects!

I ran into a math problem involving pants on Math Overflow (previously). Math Overflow is a site on which mathematicians can ask and answer each other’s questions. The question I’m talking about was asked by Tony Huynh. He knew it was possible to turn pants inside-out if your feet are tied together. (Check out the video below to see it done!) Tony was wondering if it’s possible to turn your pants around, so that you’re wearing them backwards, if your feet are tied together.

Is this possible? Another mathematician answered Tony’s question – but maybe you want to try it yourself before reading about the solution. Answering questions like this about transformations of surfaces with holes in them is part of a branch of mathematics called topology – which Euler is partly credited with starting. A more mathematical way of stating this problem is: is it possible to turn a torus (or donut) with a single hole in it inside-out? Here’s another video, by James Tanton, about turning things inside-out mathematically.

Bon appetit!

P.S. – The Math Munch team will be speaking next weekend, on April 27th, at TEDxNYED! We’re really excited to get to tell the story of Math Munch on the big stage. Thank you for being such enthusiastic and curious readers and allowing us to share our love of math with you. Maybe we’ll see some of you there!

Posted by Anna Weltman. Categories: Math Munch. Tags: Euler, graphs, history, polyhedra, primes, programming, puzzles, recreational mathematics, topology, video. 2 Comments

Feb. ’13

Folds, GIMPS, and More Billiards

Welcome to this week’s Math Munch!

First up, we’ve often featured mathematical constructions made of origami. (Here are some of those posts.) Origami has a careful and peaceful feel to it—a far cry from, say, the quick reflexes often associated with video games. I mean, can you imagine an origami video game?

One of Fold’s many origami puzzles.

Well, guess what—you don’t have to, because Folds is just that! Folds is the creation of Bryce Summer, a 21-year-old game designer from California. It’s so cool. The goal of each level of its levels is simple: to take a square piece of paper and fold it into a given shape. The catch is that you’re only allowed a limited number of folds, so you have to be creative and plan ahead so that there aren’t any loose ends sticking out. As I’ve noted before, my favorite games often require a combo of visual intuition and careful thinking, and Folds certainly fits the bill. Give it a go!

Once you’re hooked, you can find out more about Bryce and how he came to make Folds in this awesome Q&A. Thanks so much, Bryce!

Next up, did you know that a new largest prime number was discovered less than a month ago? It’s very large—over 17 million digits long! (How many pages would that take to print or write out?) That makes it way larger than the previous record holder, which was “only” about 13 million digits long. Here is an article published on the GIMPS website about the new prime number and about the GIMPS project in general.

What’s GIMPS you ask? GIMPS—the Great Internet Mersenne Primes Search—is an example of what’s called “distributed computing”. Testing whether a number is prime is a simple task that any computer can do, but to check many or large numbers can take a lot of computing time. Even a supercomputer would be overwhelmed by the task all on its own, and that’s if you could even get dedicated time on it. Distributed computing is the idea that a lot of processing can be accomplished by having a lot of computers each do a small amount of work. You can even sign up to help with the project on your own computer. What other tasks might distributed computing be useful for? Searching for aliens, perhaps?

GIMPS searches only for a special kind of prime called Mersenne primes. These primes are one less than a power of two. For instance, 7 is a Mersenne prime, because it’s one less that 8, which is the third power of 2. For more on Mersenne primes, check out this video by Numberphile.

Finally, we’ve previously shared some resources about the math of billiards on Math Munch. Below you’ll find another take on bouncing paths as Michael Moschen combines the math of billiards with the art of juggling.

So lovely. For more on this theme, here’s a second video to check out.

Bon appetit!

Posted by Justin Lanier. Categories: Math Munch. Tags: big numbers, billiards, computers, games, geometry, interactive puzzle, interview, juggling, numbers, origami, primes, video. 35 Comments