Welcome to this week’s Math Munch!
You might remember our post on Tilman Zitzmann’s project called Geometry Daily. If you haven’t seen it before, go check it out now! It will help you to appreciate Lawrie Cape’s work, which both celebrates and extends the Geometry Daily project. Lawrie’s project is called Tangent Spaces. He makes Tilman’s geometry sketches move!
 |
 |
 |
Not only do Lawrie’s sketches move, they’re also interactive—you can click on them, and they’ll move in response. All kinds of great mathematical questions can come up when you set a diagram in motion. For instance, I’m wondering what moon patterns are possible to make by dragging my mouse around—and if any are impossible. What questions come up for you as you browse Tangent Spaces?
Next up, Dorry Segev and Sommer Gentry are a doctor and a mathematician. They collaborated on a new system to help sick people get kidney transplants. They are also dance partners and husband and wife. This video shares their amazing, mathematical, and very human story.
Dorry and Sommer’s work involves building graphs, kind of like the game that Paul posted about last week. Thinking about the two of them together has been fun for me. You can read more about the life-saving power of Kidney Paired Donation on optimizedmatch.com.
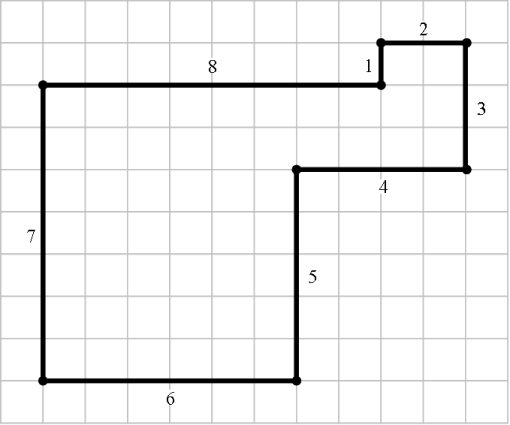
Last up this week, here’s some very fresh math—discovered in the last 24 hours! Joe O’Rourke is one of my favorite mathematicians. (previously) Joe recently asked whether a golyhedron exists. What’s a golyhedron? It’s the 3D version of a golygon. What’s a golygon? Glad you asked. It’s a grid polygon that has side lengths that grow one by one, from 1 up to some number. Here, a diagram will help:
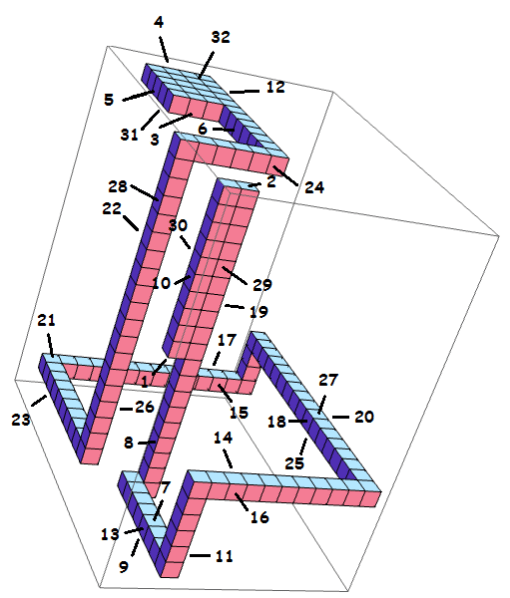
A golyhedron is like this, but in 3D: a grid shape that has one face of each area from 1 up to some number. After tinkering around some with this new shape idea, Joe conjectured that no golyhedra exist. It’s kind of like coming up with the idea of a unicorn, but then deciding that there aren’t any real ones. But Joseph wasn’t sure, so he shared his golyhedron shape idea on the internet at MathOverflow. Adam P. Goucher read the post, and decided to build a golyhedron himself.
And he found one!
Adam wrote all about the process of discovering his golyhedron in this blog post. I recommend it highly.
And the story and the math don’t stop there! New questions arise—is this the smallest golyhedron? Are there types of sequences of face sizes that can’t be constructed—for instance, what about a sequence of odd numbers? Curious and creative people, new discoveries, and new questions—that’s how math grows.
If this story was up your alley, you might enjoy checking out the story of holyhedra in this previous post.
Bon appetit!


I learned a lot in that video. The whole kidney transplant thing was pretty interesting. Basically you want to find the point with the least matches and work from there, like with the ABCD example, since B and C had two, and A and D had only one, you would match AB and CD.
Hi G,
Yeah, that was a really useful example to see how the transplant system works.Thanks for your comment and for reading Math Munch!
Justin
The video about Dorry and Sommer was super cool! It’s amazing, the complexity of the mathematic functions and systems that go into finding the right matches for people who need kidneys. The most interesting part, in my opinion, was when they explained how they also have to take into consideration the location of the potential donors and recipients. The additiion of locational logistics to the system adds an entire new realm, one that can again be navigated with math. This was a really cool and applicable real-world example of the power of mathematics and the things that it can do.
Hey Cade,
Thanks for your comment! I totally agree with your sentiments. While I love playing around in the world of “pure math”, getting to see the intricacies of Dorry and Sommer’s system is powerful and beautiful, too.
Thanks for reading Math Munch,
Justin
I thought that the video about Dorry and Sommer’s combined work was really interesting. I did not even know that kidney transplants were possible. It is incredible how many factors had to be taken into account, especially the biological ones and the issue of placement if the patients. I hope that the success that kidney transplantation has found so far continues to increase.
Thank you so much for posting the video about Dorry and Sommer’s kidney discovery, because I learned so much because this video confused me, it confused me in a somewhat a good way though; in terms of how they did it math wise I somewhat understood it not saying it was super easy to understand I still had to rewind the video sometimes because I didn’t get it when they were explaining it the first time but I got it the second or third time watching the part that confused me again, but the biology parts I did not get especially when they talking about blood type O being universal I was confused so I paused the video an googled blood type and selected the first website that popped up which was the Red Cross website which had an whole article on blood types and mix and matching them and after reading that I learned type O was an universal donor and type AB is a universal recipient but AB can sadly can only give blood to its on blood type and type O can only get blood from its own blood type but the good news is most of our population type O so usually when needing blood and being type O it is no problem and I also learned what blood types you can be when your parents are different or the same types of blood types, another thing I learned is what blood types most and least of what the U.S.A is, overall thank you sooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooo much for posting this video:).
Pingback: Nice Neighbors, Spinning GIFs, and Breakfast | Math Munch