Welcome to this week’s Math Munch!

I’ve been really into squares lately. Maybe it’s because I recently ran across a new puzzle involving squares– something called Mrs. Perkin’s quilt.

69 by 69 Mrs. Perkin’s quilt.

The original version of the puzzle was published way back in 1907, and it went like this: “For Christmas, Mrs. Potipher Perkins received a very pretty patchwork quilt constructed of 169 square pieces of silk material. The puzzle is to find the smallest number of square portions of which the quilt could be composed and show how they might be joined together. Or, to put it the reverse way, divide the quilt into as few square portions as possible by merely cutting the stitches.”

18 by 18 Mrs. Perkin’s quilt

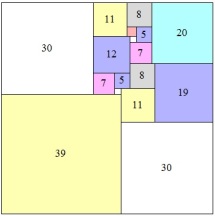
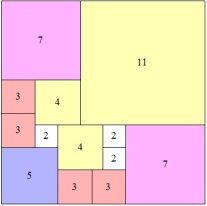
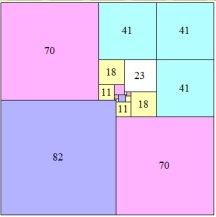
Said in another way, if you have a 13 by 13 square, how can you divide it up into the smallest number of smaller squares? Don’t worry, you get to solve it yourself– I’m not including a picture of the solution to that version of the puzzle because there are so many beautiful pictures of solutions to the puzzle when you start with larger and smaller squares. Some are definitely more interesting than others. If you want to start simple, try the 4 by 4 version. I particularly like the look of the solution to the 18 by 18 version.

152 by 152 Mrs. Perkin’s quilt

Maybe you’re wondering where I got all these great pictures of Mrs. Perkin’s quits. And– wait a second– is that the solution to the 152 by 152 version? It sure is– and I got it from one of my favorite math websites, the Wolfram Demonstrations Project. The site is full of awesome visualizations of all kinds of things, from math problems to scans of the human brain. The Mrs. Perkin’s quilts demonstration solves the puzzle for up to a 1,098 by 1,098 square!

Next up, we here at Math Munch are big fans of unusual calculators. Marble calculators, domino calculators… what will we turn up next? Well, here for your strange calculator enjoyment is a water calculator! Check out this video to see how it works:

I might not want to rely on this calculator to do my homework, but it certainly is interesting!

Finally, meet Snap the Turtle! This cute little guy is here to teach you how to make beautiful math art stars using computer programming.

On the website Tynker, Snap can show you how to design a program to make intricate line drawings– and learn something about computer programming at the same time. Tynker’s goal is to teach kids to be programming “literate.” Combine computer programming with a little math and art (and a turtle)– what could be better?

I hope something grabbed your interest this week! Bon appetit!

Welcome to this week’s Math Munch!

This week we meet an incredible mathematician, take on a tough number puzzle, check out a wonderful mathematical card trick, and much more.

A while ago we shared an interview with mathematician Fan Chung Graham.  The interview was posted by Anthony Bonato, The Intrepid Mathematician. Well, this week we share another of his interviews, this time with Maria Chudnovsky, graph theorist and star of not one, but two television commercials. (A rare feat for a mathematician.) Maria is also a winner of the extraordinary MacArthur “Genius” Grant. You can check out the video below or click here for the full interview.

Up next, our friends over at The Aperiodical do a lot of great things for the math world. One contribution is the monthly Puzzlebomb put on by Katie Steckles.

This month’s puzzle is MODOKU, a sort of sudoku style puzzle where columns and rows span the possible remainders mod 7 and mod 5. Check it out! Thanks to Katie for such a lovely puzzle! You can click below for an interactive version with complete instructions.

Finally this week, it’s time again to look at a Futility Closet, a phenomenal blog containing the odd mathematical tidbit. We’ll take a look at three of them.

Here’s a weird arithmetic fact I found there. Do you see what’s going on there? I have absolutely no idea how often this kind of thing is true, if ever again, but it gets me thinking.

Here’s another incredible one. We’ve posted about Pascal’s (Yang-Hui’s) Triangle lots of times (1 2), and I’ve come across a lot of fascinating stuff about it, but this is new to me. Apparently, “the product of the six numbers surrounding any interior number in Pascal’s triangle is a perfect square.” Can you prove it?

Now on to the biggie…  This is such a cool card trick! Here’s the trick as explained by Futility Closet:

“I hand you an ordinary deck of 52 cards. You inspect and shuffle it, then choose five cards from the deck and hand them to my assistant. She looks at them and passes four of them to me. I name the fifth card.”         !!!!!!!!!!

The key to the magic is this chart:

{low, middle, high} = 1
{low, high, middle} = 2
{middle, low, high} = 3
{middle, high, low} = 4
{high, low, middle} = 5
{high, middle, low} = 6

Can you figure out how it works from the chart alone? You’ll need a good assistant to get on board, and it wouldn’t hurt to practice a bit. Then get ready to impress. Oh, and if you can’t figure out the trick from the chart alone, then just head over to Futility Closet and read the full explanation.

Well that’s it for this week. Hope you found something delicious. Bon appetit!