Tag Archives: interview

Dots-and-Boxes, Choppy Waves, and Psi Day

Welcome to this week’s Math Munch!

And happy Psi Day! But more on that later.

Click to play Dots-and-Boxes!

Recently I got to thinking about the game Dots-and-Boxes. You may already know how to play; when I was growing up, I can only remember tic-tac-toe and hangman as being more common paper and pencil games. If you know how to play, maybe you’d like to try a quick game against a computer opponent? Or maybe you could play a low-tech round with a friend? If you don’t know how to play or need a refresher, here’s a quick video lesson:

In 1946, a first grader in Ohio learned these very same rules. His name was Elwyn Berlekamp, and he went on to become a mathematician and an expert about Dots-and-Boxes. He’s now retired from being a professor at UC Berkeley, but he continues to be very active in mathematical endeavors, as I learned this week when I interviewed him.

Elwyn Berlekamp

In his book The Dots and Boxes Game: Sophisticated Child’s Play, Elwyn shares: “Ever since [I learned Dots-and-Boxes], I have enjoyed recurrent spurts of fascination with this game. During several of these burst of interest, my playing proficiency broke through to a new and higher plateau. This phenomenon seems to be common among humans trying to master any of a wide variety of skills. In Dots-and-Boxes, however, each advance can be associated with a new mathematical insight!”

Elwyn’s booklet about
Dots-and-Boxes

In his career, Elywen has studied many mathematical games, as well as ideas in coding. He has worked in finance and has been involved in mathematical outreach and community building, including involvement with Gathering for Gardner (previously).

Elywn generously took the time to answer some questions about Dots-and-Boxes and about his career as a mathematician. Thanks, Elywn! Again, you should totally check out our Q&A session. I especially enjoyed hearing about Elwyn’s mathematical heros and his closing recommendations to young people.

As I poked around the web for Dots-and-Boxes resources, I enjoyed listening to the commentary of Phil Carmody (aka “FatPhil”) on this high-level game of Dots-and-Boxes. It was a part of a tournament held on a great games website called Little Golem where mathematical game enthusiasts from around the world can challenge each other in tournaments.

What's the best move?A Sam Loyd Dots-and-Boxes Puzzle

What’s the best move?
A Dots-and-Boxes puzzle by Sam Loyd.

And before I move on, here are two Dots-and-Boxes puzzles for you to try out. The first asks you to use the fewest lines to saturate or “max out” a Dots-and-Boxes board without making any boxes. The second is by the famous puzzler Sam Loyd (previously). Can you help find the winning move in The Boxer’s Puzzle?

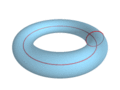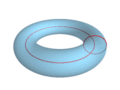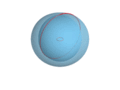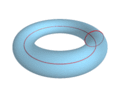
Next up, check out these fantastic “waves” traced out by “circling” these shapes:

Click the picture to see the animation!

Lucas Vieira—who goes by LucasVB—is 27 years old and is from Brazil. He makes some amazing mathematical illustrations, many of them to illustrate articles on Wikipedia. He’s been sharing them on his Tumblr for just over a month. I’ll let his images and animations speak for themselves—here are a few to get you started!

A colored-by-arc-length Archimedean spiral.

A sphere-like degenerate torus.

A Koch cube.

There’s a great write-up about Lucas over at The Daily Dot, which includes this choice quote from him: “I think this sort of animated illustration should be mandatory in every math class. Hopefully, they will be some day.” I couldn’t agree more. Also, Lucas mentioned to me that one of his big influences in making mathematical imagery has always been Paul Nylander. More on Paul in a future post!

Psi is the 23rd letter in the Greek alphabet.

Finally, today—March 11—is Psi Day! Psi is an irrational number that begins 3.35988… And since March is the 3rd month and today is .35988… of the way through it–11 out of 31 days—it’s the perfect day to celebrate this wonderful number!

What’s psi you ask? It’s the Reciprocal Fibonacci Constant. If you take the reciprocals of the Fibonnaci numbers and add them add up—all infinity of them—psi is what you get.

Psi was proven irrational not too long ago—in 1989! The ancient irrational number phi—the golden ratio—is about 1.61, so maybe Phi Day should be January 6. Or perhaps the 8th of May—8/5—for our European readers. And e Day—after Euler’s number—is of course celebrated on February 7.

That seems like a pretty good list at the moment, but maybe you can think of other irrational constants that would be fun to have a “Day” for!

And finally, I’m sure I’m not the only one who’d love to see a psi or Fibonacci-themed “Gangham Style” video. Get it?

Bon appetit!

******

EDIT (3/14/13): Today is Pi Day! I sure wish I had thought of that when I was making my list of irrational number Days…

Posted by Justin Lanier. Categories: Math Munch. Tags: art, dots-and-boxes, Fibonacci, fractals, games, interview, irrational, Martin Gardner, numbers, pi, psi, spirals, video, waves. 24 Comments

Feb. ’13

Marjorie Rice, Inspired by Math, and Subways

Welcome to this week’s Math Munch!

A few weeks ago, I learned about an amazing woman named Marjorie Rice. Marjorie is a mathematician – but with a very unusual background.

Marjorie had no mathematical education beyond high school. But, Marjorie was always interested in math. When her children were all in school, Marjorie began to read about and work on math problems for fun. Her son had a subscription to Scientific American, and Marjorie enjoyed reading articles by Martin Gardner (of hexaflexagon fame). One day in 1975, she read an article that Martin Gardner wrote about a new discovery about pentagon tessellations. Before several years earlier, mathematicians had believed that there were only five different types of pentagons that could tessellate – or cover the entire plane without leaving any gaps. But, in 1968, three more were discovered, and, in 1975, a fourth was found – which Martin Gardner reported on in his article.

When she read about this, Marjorie became curious about whether she could find her own new type of pentagon that could tile the plane. So, she got to work. She came up with her own notation for the relationships between the angles in her pentagons. Her new notation helped her to see things in ways that professional mathematicians had overlooked. And, eventually… she found one! Marjorie wrote to Martin Gardner to tell him about her discovery. By 1977, Marjorie had discovered three more types of pentagons that tile the plane and her new friend, the mathematician Doris Schattschneider, had published an article about Marjorie’s work in Mathematics Magazine.

There are now fourteen different types of pentagons known to tile the plane… but are there more? No one knows for sure. Whether or not there are more types of pentagons that tile the plane is what mathematicians call an open problem. Maybe you can find a new one – or prove that one can’t be found!

Marjorie has a website called Intriguing Tessellations on which she’s written about her work and posted some of her tessellation artwork. Here is one of her pentagon tilings transformed into a tessellation of fish.

By the way, it was Marjorie’s birthday a few weeks ago. She just turned 90 years old. Happy Birthday, Marjorie!

$wild about math logo$ Next up, I just ran across a great blog called Wild About Math! This blog is written by Sol Lederman, who used to work with computers and LOVES math. My favorite part about this blog is a series of interviews that Sol calls, “Inspired by Math.” Sol has interviewed about 23 different mathematicians, including Steven Strogatz (who has written two series of columns for the New York Times about mathematics) and Seth Kaplan and Deno Johnson, the producer and writer/director of the Flatland movies. You can listen to Sol’s podcasts of these interviews by visiting his blog or iTunes. They’re free – and very interesting!

Finally, what New York City resident or visitor isn’t fascinated by the subway system? And what New York City resident or visitor doesn’t spend a good amount of time thinking about the fastest way to get from point A to point B? Do you stay on the same train for as long as possible and walk a bit? Or do you transfer, and hope that you don’t miss your train?

Chris and Matt, on the subway.

Well, in 2009, two mathematicians from New York – Chris Solarz and Matt Ferrisi – used a type of mathematics called graph theory to plan out the fastest route to travel the entire New York City subway system, stopping at every station. They did the whole trip in less than 24 hours, setting a world record! Graph theory is the branch of mathematics that studies the connections between points or places. In their planning, Chris and Matt used graph theory to find a route that had the most continuous travel, minimizing transfers, distance, and back-tracking. You can listen to their fascinating story in an interview with Chris and Matt done by the American Mathematical Society here.

If you’re interested in how graph theory can be used to improve the efficiency of a subway system, check out this article about the Berlin subway system (the U-bahn). Students and professors from the Technical University Berlin used graph theory to create a schedule that minimized transfer time between trains. If only someone would do this in New York…

Bon appetit!

Posted by Anna Weltman. Categories: Math Munch. Tags: art, geometry, graphs, history, interview, Martin Gardner, open problem, podcast, tessellation. 14 Comments

Feb. ’13

Folds, GIMPS, and More Billiards

Welcome to this week’s Math Munch!

First up, we’ve often featured mathematical constructions made of origami. (Here are some of those posts.) Origami has a careful and peaceful feel to it—a far cry from, say, the quick reflexes often associated with video games. I mean, can you imagine an origami video game?

One of Fold’s many origami puzzles.

Well, guess what—you don’t have to, because Folds is just that! Folds is the creation of Bryce Summer, a 21-year-old game designer from California. It’s so cool. The goal of each level of its levels is simple: to take a square piece of paper and fold it into a given shape. The catch is that you’re only allowed a limited number of folds, so you have to be creative and plan ahead so that there aren’t any loose ends sticking out. As I’ve noted before, my favorite games often require a combo of visual intuition and careful thinking, and Folds certainly fits the bill. Give it a go!

Once you’re hooked, you can find out more about Bryce and how he came to make Folds in this awesome Q&A. Thanks so much, Bryce!

Next up, did you know that a new largest prime number was discovered less than a month ago? It’s very large—over 17 million digits long! (How many pages would that take to print or write out?) That makes it way larger than the previous record holder, which was “only” about 13 million digits long. Here is an article published on the GIMPS website about the new prime number and about the GIMPS project in general.

What’s GIMPS you ask? GIMPS—the Great Internet Mersenne Primes Search—is an example of what’s called “distributed computing”. Testing whether a number is prime is a simple task that any computer can do, but to check many or large numbers can take a lot of computing time. Even a supercomputer would be overwhelmed by the task all on its own, and that’s if you could even get dedicated time on it. Distributed computing is the idea that a lot of processing can be accomplished by having a lot of computers each do a small amount of work. You can even sign up to help with the project on your own computer. What other tasks might distributed computing be useful for? Searching for aliens, perhaps?

GIMPS searches only for a special kind of prime called Mersenne primes. These primes are one less than a power of two. For instance, 7 is a Mersenne prime, because it’s one less that 8, which is the third power of 2. For more on Mersenne primes, check out this video by Numberphile.

Finally, we’ve previously shared some resources about the math of billiards on Math Munch. Below you’ll find another take on bouncing paths as Michael Moschen combines the math of billiards with the art of juggling.

So lovely. For more on this theme, here’s a second video to check out.

Bon appetit!

Posted by Justin Lanier. Categories: Math Munch. Tags: big numbers, billiards, computers, games, geometry, interactive puzzle, interview, juggling, numbers, origami, primes, video. 35 Comments