Welcome to this week’s Math Munch.
I was saddened to learn this week of the passing of Solomon Golomb.
Can you imagine the world without Tetris? What about the world without GPS or cell phones?
Here at Math Munch we are big fans of pentominoes and polyominoes—we’ve written about them often and enjoy sharing them and tinkering with them. While collections of glued-together squares have been around since ancient times, Solomon invented the term “polyominoes” in 1953, investigated them, wrote about them—including this book—and popularized them with puzzle enthusiasts. But one of Solomon’s outstanding qualities as a mathematician is that he pursued a range of projects that blurred the easy and often-used distinction between “pure” and “applied” mathematics. While polyominoes might seem like just a cute plaything, Solomon’s work with discrete structures helped to pave the way for our digital world. Solomon compiled the first book on digital communications and his work led to such technologies as radio telescopes. You can hear him talk about the applications that came from his work and more in this video:
Here is another video, one that surveys Solomon’s work and life. It’s fast-paced and charming and features Solomon in a USC Trojan football uniform! Here is a wonderful short biography of Solomon written by Elwyn Berlekamp. And how about a tutorial on a 16-bit Fibonacci linear feedback shift register—which Solomon mentions as the work he’s most proud of—in Minecraft!
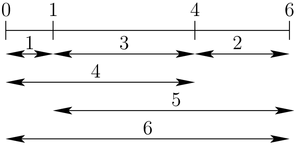
Another kind of mathematical object that Solomon invented is a Golomb ruler. If you think about it, an ordinary 12-inch ruler is kind of inefficient. I mean, do we really need all of those markings? It seems like we could just do away with the 7″ mark, since if we wanted to measure something 7 inches long, we could just measure from the 1″ mark to the 8″ mark. (Or from 2″ to 9″.) So what would happen if we got rid of redundancies of this kind? How many marks do you actually need in order to measure every length from 1″ to 12″?
I was pleased to find that there’s actually a distributed computing project at distributed.net to help find new Golomb Rulers, just like the GIMPS project to find new Mersenne primes. It’s called OGR for “Optimal Golomb Ruler.” Maybe signing up to participate would be a nice way to honor Solomon’s memory. It’s hard to know what to do when someone passionate and talented and inspiring dies. Impossible, even. We can hope, though, to keep a great person’s memory and spirit alive and to help continue their good work. Maybe this week you’ll share a pentomino puzzle with a friend, or check out the sequences on the OEIS that have Solomon’s name attached to them, or host a Tetris or Blokus party—whatever you’re moved to do.
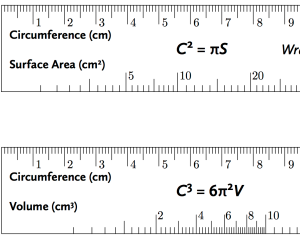
Thinking about Golomb rulers got me to wondering about what other kinds of nifty rulers might exist. Not long ago, at Gathering for Gardner, Matt Parker spoke about a kind of ruler that foresters use to measure the diameter of tree. Now, that sounds like quite the trick—seeing how the diameter is inside of the tree! But the ruler has a clever work-around: marking things off in multiples of pi! You can read more about this kind of ruler in a blog post by Dave Richeson. I love how Dave got inspired and took this “roundabout ruler” idea to the next level to make rulers that can measure area and volume as well. Generalizing—it’s what mathematicians do!
 |
 |
I was also intrigued by an image that popped up as I was poking around for interesting rulers. It’s called a seam allowance curve ruler. Some patterns for clothing don’t have a little extra material planned out around the edges so that the clothes can be sewn up. (Bummer, right?) To pad the edges of the pattern is easy along straight parts, but what about curved parts like armholes? Wouldn’t it be nice to have a curved ruler? Ta-da!
Speaking of Gathering for Gardner: it was announced recently that G4G is helping to sponsor an online puzzle challenge called 52 Master Pieces. It’s an “armchair puzzle hunt” created by David Cohen, a physician in Atlanta. It will all happen online and it’s free to participate. There will be lots of puzzle to solve, and each one is built around the theme of a “master” of some occupation, like an architect or a physician. Here are a couple of examples:
 |
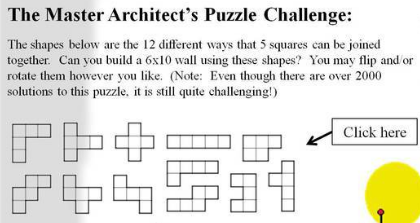 |
Notice that both of these puzzles involve pentominoes!
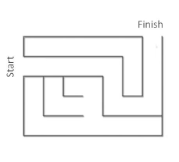
The official start date to the contest hasn’t been announced yet, but you can get a sneak peek of the site—for a price! What’s the price, you ask? You have to solve a puzzle, of course! Actually, you have your choice of two, and each one is a maze. Which one will you pick to solve? Head on over and give it a go!
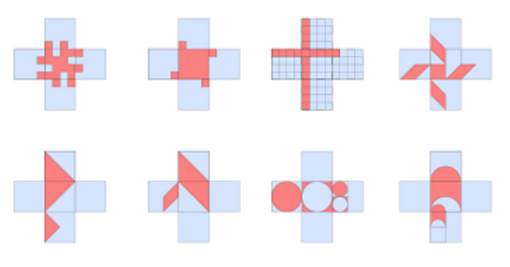
And one last thing before I go: if you’re intrigued by that medicine puzzle, you might really like checking out 100 different ways this shape can be 1/4 shaded. They were designed by David Butler, who teaches in the Maths Learning Centre at the University of Adelaide. Which one do you like best? Can you figure out why each one is a quarter shaded? It’s like art and a puzzle all at once! Can you come up with some quarter-shaded creations of your own? If you do, send them our way! We’d love to see them.
Bon appetit!