Tag Archives: applet

01

Oct. ’12

Rectangles, Explosions, and Surreals

Welcome to this week’s Math Munch!

What is 3 x 4?   3 x 4 is 12.

Well, yes. That’s true. But something that’s wonderful about mathematics is that seemingly simple objects and problems can contain immense and surprising wonders.

How many squares can you find in this diagram?

As I’ve mentioned before, the part of mathematics that works on counting problems is called combinatorics. Here are a few examples for you to chew on: How many ways can you scramble up the letters of SILENT? (LISTEN?) How many ways can you place two rooks on a chessboard so that they don’t attack each other? And how many squares can you count in a 3×4 grid?

Here’s one combinatorics problem that I ran across a while ago that results in some wonderful images. Instead of asking about squares in a 3×4 grid, a team at the Dubberly Design Office in San Francisco investigated the question: how many of ways can a 3×4 grid can be partitioned—or broken up—into rectangles? Here are a few examples:

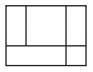How many different ways to do this do you think there are? Here’s the poster that they designed to show the answer that they found! You can also check out this video of their solution.

In their explanation of their project, the team states that “Design tools are becoming more computation-based; designers are working more closely with programmers; and designers are taking up programming.” Designing the layout of a magazine or website requires both structural and creative thinking. It’s useful to have an idea of what all the possible layouts are so that you can pick just the right one—and math can help you to do it!

If you’d like to try creating a few 3×4 rectangle partitions of your own, you can check out www.3x4grid.com. [Sadly, this page no longer works. See an archive of it here. -JL, 10/2016]

Next up, explosions! I could tell you about the math of the game Minesweeper (you can play it here), or about exploding dice. But the kind of explosion I want to share with you today is what’s called a “combinatorial explosion.” Sometimes a problem that appears to be an only slightly harder variation of an easy problem turns out to be way, way harder. Just how BIG and complicated even simple combinatorics problems can get is the subject of this compelling and also somewhat haunting video.

Donald Knuth

Finally, all of this counting got me thinking about big numbers. Previously we’ve linked to Math Cats, and Wendy has a page where you can learn how to say some really big numbers. But thinking about counting also made me remember an experience I had in middle school where I found out just how big numbers could be! I was in seventh grade when I read this article from the December 1995 issue of Discover Magazine. It’s called “Infinity Plus One, and Other Surreal Numbers” and was written by Polly Shulman. I remember my mind being blown by all of the talk of infinitely-spined aliens and up-arrow notation for naming numbers. Here’s an excerpt:

“Mathematicians and precocious five-year-olds have long been fascinated by the endlessness of numbers, and they’ve named the endlessness infinity. Infinity isn’t a number like 1, 2, or 3; it’s hard to say what it is, exactly. It’s even harder to imagine what would happen if you tried to manipulate it using the arithmetic operations that work on numbers. For example, what if you divide it in half? What if you multiply it by 2? Is 1 plus infinity greater than, less than, or the same size as infinity plus 1? What happens if you subtract 1 from it?”

After I read this article, John Conway and Donald Knuth became heros of mine. (In college, I had the amazing fortune to have breakfast with Conway one day when he was visiting to give a lecture!) Knuth has a book about surreals that’s the friendliest introduction to the surreal numbers that I know of, and in this video, Vi Hart briefly touches on surreal numbers in discussing proofs that .9 = 1. Boy, would I love to see a great video or online resource that simply and beautifully lays out the surreal numbers in all their glory!

It was fun for me to remember that Discover article. I hope that you, too, run across some mathematics that leaves a seventeen-year impression on you!

Bon appetit!

Posted by . Categories: Math Munch. Tags: , , , , , , , , , . 4 Comments

09

Sep. ’12

Algorithmic House, Billiards, and Picma

Welcome to this week’s Math Munch!

Check out this beautiful building:

This is the Endesa Pavilion, located in Barcelona, Spain.  It’s also called Solar House 2.0, and that’s because the tops of all of those pyramid-spikes are covered in solar panels.  But that’s not all – this house was designed to best capture sunlight in the exact location it was built using a mathematical algorithm.

To build this house, architect Rodrigo Rubio, who works for the Institute for Advanced Architecture of Catalonia, first tracked the path of the sun over the spot he wanted to build the house.  He then plugged that data into a computer program.  This program is a set of mathematical steps called an algorithm that turns data about the movement of the sun in the sky into a geometric building.  The building it creates is the best – or optimal – building for that spot.

It puts solar panels in locations on the building that get the most sunlight and orients them to get the most exposure.  It places windows of different sizes and overhangs at different angles around the house to get the best ventilation, block sunlight from entering the house, and keep the house cool in the summer and warm in the winter.   And, because it’s an algorithm, it can be used to design the optimal house for any location.  The program then creates a pattern for the wooden pieces that make up the house.  This pattern can be sent to a machine that cuts out the pieces, which builders put together like a puzzle.

In this video, Rodrigo explains how the building was designed, how the design works, and how this design can be used to make eco-friendly houses all over the world.

[youtube http://www.youtube.com/watch?v=3R1CBFBxuew&feature=player_embedded]

Next, have you ever played billiards?  Maybe you’ve played pool or watched Donald Duck play billiards.  It’s interesting to see how a pool ball moves around on a rectangular billiards table, which is how the table is usually shaped.  But it’s even more interesting to see how a ball moves around on a triangular, pentagonal, circular, or elliptical billiards table!

Want to try?  Check out this series of applets from Serendip, an exploratory math and science website started by some professors at Bryn Mawr College in Pennsylvania.  Serendip aims to help people ask and answer their own questions about the world we live in.  In these billiards applets, you can explore dynamical systems – mathematical structures in which an object moves according to a rule.   In some situations, the object will move in a predictable way.  But in other situations, the object moves chaotically.  As you play with the applets, see if you can figure out how the shape of the table effects whether the billiard ball will move chaotically or predictably.  These applets also make some beautiful star-like designs!

Finally, here’s a new game: Picma Squared.  In this game, you use logic to figure out how to color the squares in the grid to make a picture.  It starts out simple, but the higher levels are really challenging!  Enjoy!


Look for this game and others on our Games page!

 

 

Bon appetit!

Posted by . Categories: Math Munch. Tags: , , , , , . 7 Comments

03

Sep. ’12

Demonstrations, a Number Tree, and Brainfilling Curves

Welcome to this week’s Math Munch!

Maybe you’re headed back to school this week. (We are!) Or maybe you’ve been back for a few weeks now. Or maybe you’ve been out of school for years. No matter which one it is, we hope that this new school year will bring many new mathematical delights your way!

A website that’s worth returning to again and again is the Wolfram Demonstrations Project (WDP). Since it was founded in 2007, users of the software package Mathematica have been uploading “demonstrations” to this website—amazing illuminations of some of the gems of mathematics and the sciences.

Each demonstration is an interactive applet. Some are very simple, like one that will factor any number up to 10000 for you. Others are complex, like this one that “plots orbits of the Hopalong map.”

Some demonstrations are great for visualizing facts about math, like these:

Any Quadrilateral Can Tile

A Proof of Euler’s Formula

Cube Net or Not?

There’s also a whole category of demonstrations that can be used as MArTH—mathematical art—tools, including these:

Rotate and Fold Back

Polygons Arranged in a Circle

Turtle Fractals

With over 8000 demonstrations to explore and new ones being added all the time, you can see why the Wolfram Demonstrations Project is worth returning to again and again!

Jeffrey Ventrella’s Number Tree

Next up, check out this number tree. It was created by Jeffrey Ventrella, an innovator, artist, and computer programmer who lives in San Francisco. His number tree arranges the numbers from 1 to 100 according to their largest proper factors. For instance, the factors of 18 are 18, 9, 6, 3, 2, and 1. Once we toss out 18 itself as being “improper”—a.k.a. “uninteresting”—the largest factor of 18 is 9. This in turn has as its largest factor 3, and 3 goes down to 1. Chains of factors like this one make up Jeffrey’s tree. It has a wonderful accumulative feeling to it—it’s great to watch how patterns and complexity build up over time.

(On this theme, WDP also has a demonstrations about trees and about prime factorization graphs.)

Cloctal: “a fractal design that visualizes the passage of time”

There’s lots more math to explore on Jeffrey’s website. His piece Cloctal—a fractal clock—is one of my favorites. What I’d like to feature here, though, is the diverse and intricate work Jeffrey has done with plane-filling and space-filling curves.  You can find many examples at fractalcurves.com, Jeffrey’s website that’s chock full of great links.

Jeffrey recently completed a book called Brainfilling Curves. It’s “a visual math expedition, lead by a lifelong fractal explorer.” According to the description, the book picks up where Mandelbrot left off and develops an intuitive scheme for understanding an “infinite universe of fractal beauty.”

An example of a “brainfilling curve” from Jeffrey’s “root8” family

The title comes from the idea that nature uses space-filling curves quite often, to pack intestines into your gut or lots and lots of tissue into the brain you’re using to read this right now! Hopefully you’re finding all of this math quite brainfilling as well.

(And just one more example of why WDP is worth revisiting: here’s a demonstration that depicts the space-filling Hilbert and Moore curves. So much good stuff!)

Finally, here’s a video that Jeffrey made about brainfilling curves. You can find more on his YouTube channel.

Bon appetit!

Posted by . Categories: Math Munch. Tags: , , , , , , , , , , , , , . 3 Comments